1. 연속형 확률변수
2. 균일분포
3. 정규분포
4. 지수분포
5장에 이어 모집단과 관련된 내용이다.
1. 연속형 확률변수
- 주어진 구간에 대한 적분으로 확률을 계산하며, 특정 변수에 대한 확률은 0이다.(변수 값이 무한대이기 때문)
- 확률질량함수x -> 확률밀도함수
- 예: 균일분포, 정규분포, 지수분포, 베타분포, 감마분포, t분포, 카이제곱분포, F분포 등 (이산형 확률분포의 예와 겹치는 것은 균일분포 뿐)
(*균일분포: 모든 값이 동일한 확률을 가지는 분포) - X의 확률밀도함수: P(a ≤ X ≤ b)= $ \int_{a}^{b}f(x)dx $
- 성질 1) 모든 실수 값 x에 대해 f(x) ≥ 0
- 성질 2) $ \int_{-∞}^{∞}f(x)dx = 1 $
- <주의> P(a<X<b) = P(a≤X≤b) (특정 상수값을 가질 확률이 0이라서)
- 누적분포함수: $ F(x) = P(-∞ < X ≤ x) = \int_{ -∞}^{x}f(x)dx $
- 평균: E(X) = $ \int_{-\infty}^{\infty}xf(x)dx $
- 분산: $ \int_{-\infty}^{\infty}(x-u)^2f(x)dx $ = $ \int_{-\infty}^{\infty}x^2f(x)dx $ - $ (\int_{-\infty}^{\infty}xf(x)dx)^2 $
2. 균일분포
- 균일분포: 확률밀도함수가 정의되는 구간 안에서, 똑같은 높이로 일정한 확률분포 / u(a,b)로 표시, (a,b)는 구간
- 특정 구간에 속하는 확률은 전체 구간의 길이와 특정구간의 길이의 비에 비례함.
- E(X) = (a+b)/2, V(X) = (b-a)^2 / 12
3. 정규분포
- 확률밀도함수 형태: 중간이 볼록한 종모양의 정규곡선으로 표현됨
- 식: $ f(x)=\frac{1}{\sigma\sqrt{2\pi }} exp(-\frac{(x-u)^2}{2\sigma ^2}) $ (단, -무한대< x, u < 무한대, σ > 0
==> 확률변수 X는 평균이 u이고, 분산이 $ σ^2 $인 정규분포라 하고, N(u, $ σ^2 $) 으로 표현.
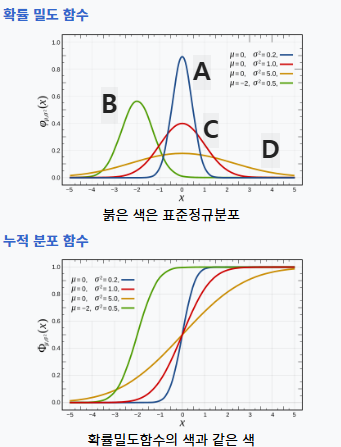
정규분포의 특성
- u가 평균, 최빈값(가장 큰값), 중앙값이고, u에 대해 대칭이다.
평균과 분산이 다른 함수
- A-C-D는 평균이 같고, 분산이 다름, B-C는 분산이 유사, 평균이 다름
정규곡선 부분 넒이
- u ± σ = 68.3%u ± 1.96 σ = 95%u ± 2σ = 95.4%u ± 3σ = 99.7%
표준 정규분포
- u = 0, σ = 1인 정규분포
- 표현: 확률변수는 Z, 확률밀도함수: ∮(z), 누적분포함수: $\Phi$(z)
- 함수: $ f(x)=\frac{1}{\sqrt{2\pi }} exp(-\frac{z^2}{2}) $
- 넓이 계산: 정확한 정적분함수 보다는 '표준정규확률분포표'를 활용하여 누적분포함수값을 사용함. (위에 언급한 정규곡선 부분 넓이 처럼)
- 표준정규분포화 하는 법: (X-u) / σ
이항분포의 정규근사
- np, n(1-p) >= 5 일때, P(a≤X≤b) = P((a-u)/ σ ≤Z≤(b-u)/ σ ) $\approx $ $ \Phi ((\frac{b+0.5-u}{\sigma}) - \Phi (\frac{a-0.5-u}{\sigma}) $
- 더하고 빼진 0.5는 연속성 수정계수이다.
- a포함, b비포함 -> b-0.5, a-0.5 / a비포함, b포함 -> +,+ / a,b 비포함 -> -,+
4. 지수분포
- 랜덤 시간의 분포, 무기억성을 가짐(예, 전구의 수명)
- 무기억성: 앞으로 1년동안 교통사고를 당할 확률은, 10년간 교통사고를 당하지 않은 사람과, 방금 교통사고를 당한 사람에게 똑같이 적용된다고 가정하는 경우, 교통사고를 당하는데 걸리는 시간은 무기억성을 가진다고 할 수 있음
'통계 > 통계_EXCEL.SPSS.R로 배우는 통계학 입문' 카테고리의 다른 글
| [통계/기초] #8 추정 (0) | 2025.05.11 |
|---|---|
| [통계/기초] #7 표본추출과 표집분포형 (2) | 2025.05.09 |
| [통계/기초] #5 이산형 확률변수 (0) | 2025.05.08 |
| [통계/기초] #4 확률 (0) | 2025.05.07 |
| [통계/기초] #3 수치 기술통계 (0) | 2025.05.07 |


